L2R(learning to rank)是指利用机器学习的技术,去完成排序的任务。在模型训练阶段,该算法最终优化的目标是一个更加合理的排序指标。L2R技术已经成功应用在信息检索(IR)、NLP、和数据挖掘(DM)等领域【1】。根据具体优化的目标不同,L2R算法主要分为Pointwise,Pairwise,Listwise三类。本文首先介绍L2R建模的整体框架,然后针对三类方法分别进行介绍。
L2R建模
L2R建模的基本框架如下所示:
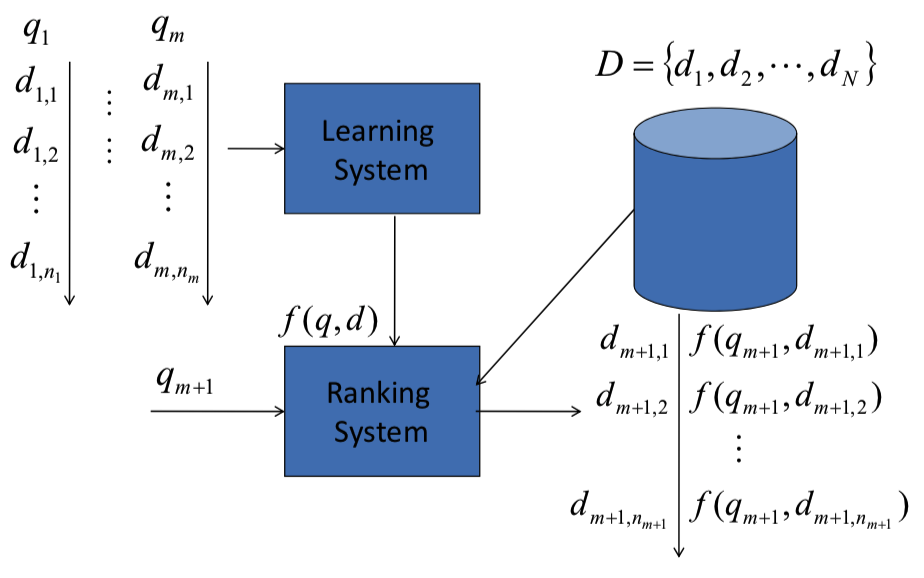
如图1所示,模型具体分为训练和预测两个解读。
训练阶段: 训练数据包括多个group, 其中每个group由1个query和1组document共同构成。该group中,$q_i$表示第$i$个query,$d_{i,j}$表示对应第$i$个query的第$j$个document, 不仅包含了document的各种属性,也包括了对应document和query之间的相关性标签$y_i$。具体如下所示:
$S=[((q_1, D_1), y_1), ((q_2, D_2), y_2), …, ((q_m, D_m), y_m)]$
$D_i=[d_{i,1}, d_{i,2}, …, d_{i,n}]$
$y_i=[y_{i,1}, y_{i,2}, …, y_{i,n}]$
其中$m$表示query个数,$n$表示每个group的document个数(此处假设每个group的document个数相同为$n$)
在训练阶段,每个pair$(q_i$, $d_{i,j})$ 都提取相关的特征,作为特征向量$x_{i,j}$。 模型学习的目标是,对每个pair$(q_i$, $d_{i,j})$,预测其对应的分数$f(x_{i,j})$, 使得根据这些分数得到的每个$q_i$对应的所有$d_{i,j}$排序尽量接近真实排序。
预测阶段: 输入query $q_{m+1}$和document集合$D=[d_1, d_2, … , d_N]$, 利用训练得到的model,预测query $q_{m+1}$和每个document $d_i$的相关性分数,并根据预测的分数对document进行排序,输出排序列表。
和分类回归的关系: 传统的分类和回归方法,通过学习相关模型,预测样本的类别或者分数值;而排序模型,则是通过模型,预测样本相关性(或者其它分数)的相对顺序。在分类问题中,有一种问题是序数分类(Ordinal Classification),序数分类问题和排序问题有点类似,不同之处在于序数分类的目标是预测顺序的类别(ordered-categorization of objects),而排序问题的目标是预测相对顺序(ordering)。
L2R评估
L2R的评估基于预测的rank list和真实的rank list比较,主要有DCG(Discounted Cumulative Gain),NDCG(Normalized Discounted Cumulative Gain),MAP(Mean Average Precision)等评估指标。
DCG
对于给定的query, TOP T的返回结果对应的DCG值如下所示:
$DCG@T = \sum_{i=1}^T \frac{2^{l_i} - 1}{log(1 + i)} $
其中$i$表示预测结果列表中第$i$个位置,$l_i$表示预测结果中第$i$个位置的document的真实相关性值。分子部分描述了饭回结果的相关性,分母部分针对位置进行加权,排序越靠前,其对应的相关性值权重系数越大。
所有query的平均DCG值作为最终排序系统DCG评估值。
NDCG
NDCG在DCG指标基础上进行了扩展,通过将DCG值除于DCG最佳排序对应的DCG值,将其归一化到0-1的范围,其定义如下所示:
$NDCG@T = \frac{DCG@T}{maxDCG@T} $
所有query的平均NDCG值作为最终排序系统DCG评估值。
MAP
map是L2R中另一种评估指标,其对应的相关性标签只有0和1。对于给定的query,AP的定义如下所示:
$AP = \frac{\sum_{i=1}^{n} P(i) * l_i}{\sum_{i=1}^{n}l_i}$
其中$i$表示预测结果列表中第$i$个位置,$l_i$表示预测结果中第$i$个位置的document的真实相关性值(在MAP中,相关性值取0或1)。$n$表示排序列表的长度,$P(i)$表示从列表第一个位置到第$i$个位置预测结果的平均准确率,其定义如下:
$P(i) = \frac{\sum_{k=1}^i l_k}{i}$
所有query的平均AP值作为最终排序系统MAP评估值。
Pointwise
在Pointwise方法中,排序问题可以转化成分类或回归问题,分类(包括序数分类)或回归的方法都可以使用。由于建模没有使用样本的相对顺序,group也不需要构建。
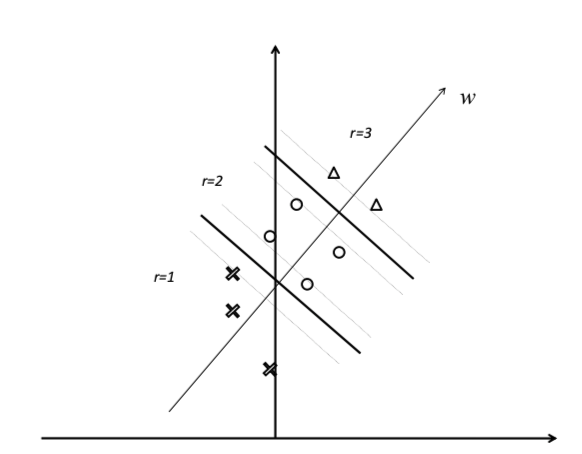
此处以OC SVM(SVM for Ordinal Classification)【2】为例,说明如何利用分类方法解决排序问题。该方法优化的目标是,对于任何相邻的2个类别,最大化其对应的分类间隔。实现层面,如图2所示,对于类别为$l$的序数分类问题,引用$l-1$个分类器 $⟨w, x⟩−b_r(r = 1,···,l − 1)$, 其中$ b_1≤···≤b_{l−1}≤b_l=\inf $。$⟨w, x⟩−b_r = 0$用于划分第$r$和$r-1$个类别,如果$⟨w, x⟩ + b_{r-1} >= 0$并且$⟨w, x⟩ + b_{r} < 0$, 则样本标签属于$y=r$。建模的目标函数如下所示:
$min_{w, b, \xi} = \frac{1}{2}||w||^2+C\sum_{r=1}^{l-1}\sum_{i=1}^{m_r}(\xi_{r,i}+\xi_{r+1,i}^*)$
约束如下:
$⟨w, x_{r, i}⟩ + b_r < -(1 - \xi_{r,i})$
$⟨w, x_{r+1, i}⟩ + b_r >= 1 - \xi_{r, i}^*$
$\xi_{r,i} >= 0$
$\xi_{r+1,i}^* >= 0$
$i = 1, 2, … , m_r$
$r = 1, 2, …, l-1$
$m = m_1 + m_2 + … + m_l$
其中 $x_{r,i}$表示第$r$个类别的第$i$个样本,$\xi_{r,i}$和$\xi_{r+1,i}^*$表示对应的松弛变量,$m$是样本的个数, $m_i$表示第$i$类样本的个数。
Pairwise
基于pairwise的rank方法中,将排序问题转化为pairwise的分类或回归问题进行求解。通常情况下,针对一个query对应的document pair, 利用分类器对pair的order进行判断。常见的pairwise rank方法有RankNet、RankSvm等,此处以RankNet为例进行说明。
RankNet原理及求解
RankNet建模
RankNet使用的打分模型要求对参数可导,训练数据根据query分为多个组,对于1个给定的query,选择2个不同相关性label的document pair,计算相关性分数$s_i=f(x_i)$和$s_j=f(x_j)$,RankNet对其对应的特征向量进行打分。$d_i>d_j$表示document $d_i$的相关性大于$d_j$。
document $d_i$的相关性大于document $d_j$的概率如下:
$P_{ij}=P(d_i>d_j)=\frac{1}{1+e^{-\sigma (s_i-s_j)}} (1)$
其中$\sigma$是常数,决定sigmoid函数的形状。RankNet采用交叉熵函数训练模型,如下所示。其中$P’_{ij}$表示真实的$d_i$相关性大于$d_j$的概率。
$C=-P’_{ij}logP_{ij}-(1-P’_{ij})log(1-P_{ij}) (2)$
RankNet求解
为方便后续描述,针对1个给定的query,我们定义变量$S_{ij}$:
$S_{ij} =
\begin{cases}
1, & d_i比d_j更相关\\
-1, & d_j比d_i更相关\\
0 & d_i和d_j相关性相同
\end{cases}
(3)$
在本文中,假定对于每个query,其对应所有document的相关性顺序都是完全确定的。
因此,
$P’_{ij}=\frac{1}{2}(1+S_{ij}). (4)$
由上述式2和式4可以得出:
$C=-P’_{ij}logP_{ij}-(1-P’_{ij})log(1-P_{ij}) \\
= -\frac{1}{2}(1+S_{ij})logP_{ij}-(1-\frac{1}{2}(1+S_{ij}))log(1-P_{ij}) \\
= -\frac{1}{2}(logP_{ij}+log(1-P_{ij}))-\frac{1}{2}S_{ij}(logP_{ij}-log(1-P_{ij}) \\
= -\frac{1}{2}log(P_{ij}*(1-P_{ij}))-\frac{1}{2}S_{ij}log\frac{P_{ij}}{1-P_{ij}} \\
= -\frac{1}{2}log\frac{e^{-\sigma(s_i-s_j)}}{(1+e^{-\sigma(s_i-s_j)})^2} -\frac{1}{2}S_{ij}loge^{\sigma(s_i-s_j)} \\
= -\frac{1}{2}(-\sigma(s_i-s_j)-2log(1+e^{-\sigma(s_i-s_j)})) -\frac{1}{2}S_{ij}\sigma(s_i-s_j) \\
= \frac{1}{2}(1-S_{ij})\sigma(s_i-s_j)+log(1+e^{-\sigma(s_i-s_j})
(5)$
$C =
\begin{cases}
log(1+e^{-\sigma(s_i-s_j)}), & 当S_{ij}=1\\
log(1+e^{-\sigma(s_j-s_i)}), & 当S_{ij}=-1
\end{cases}
(6)$
$C$对$s$求导,结果如下:
$ \frac{\varphi C}{\varphi s_i}=\sigma (\frac{1}{2}(1-S_{ij})-\frac{1}{1+e^{-\sigma(s_i-s_j)}})=-\frac{\varphi C}{\varphi s_j} (7)$
通过SGD的方式进行求解
$w_k=w_k-\eta (\frac{\varphi C}{\varphi s_i}\frac{\varphi s_i}{\varphi w_k}+\frac{\varphi C}{\varphi s_j}\frac{\varphi s_j}{\varphi w_k}) (8)$
其中$\eta > 0$为学习率。
RankNet求解加速
对于给定的文档对$d_i$和$d_j$,
$ \frac{\varphi C}{\varphi w_k}=\frac{\varphi C}{\varphi s_i}\frac{\varphi s_i}{w_k}+\frac{\varphi C}{\varphi s_j}\frac{\varphi s_j}{\varphi w_k} = \sigma (\frac{1}{2}(1-S_{ij})-\frac{1}{1+e^{-\sigma(s_i-s_j)}}) (\frac{\varphi s_i}{\varphi w_k} - \frac{\varphi s_j}{\varphi w_k})=\lambda_{ij}(\frac{\varphi s_i}{\varphi w_k} - \frac{\varphi s_j}{\varphi w_k})(9)$
其中$\lambda_{ij}=\frac{\varphi C}{\varphi s_i}= \sigma (\frac{1}{2}(1-S_{ij})-\frac{1}{1+e^{-\sigma(s_i-s_j)}})(10)$
我们定义$I$为索引对$(i,j)$的集合(其中$doc_i$的相关性大于$doc_j$),汇总来自所有文档对的贡献,
$\delta w_k=-\eta \sum_{(i,j) \in I} \lambda_{ij}(\frac{\varphi s_i}{\varphi w_k} - \frac{\varphi s_j}{\varphi w_k})=-\eta\sum_i\lambda_i\frac{\varphi s_i}{\varphi w_k}(11)$
其中$\lambda_i = \sum_{j:(i,j) \in I}\lambda_{ij}-\sum_{j:(j,i) \in I}\lambda_{ij}$,每个document对应一个$\lambda_i$,其含义为损失函数对文档$d_i$的模型打分$s_i$的梯度。方向表示梯度的方向,大小表示梯度的幅度。每个$\lambda_i$的计算都来自该document对应的所有pair。在实际计算时,可以对每个文档计算其对应的$\lambda_i$,然后用于更新模型参数。这种mini-batch的梯度更新方式和问题分解方法,显著提升了RankNet模型训练的效率。
Listwise
基于pairwise的方法(如RankNet)优化的是pairwise误差,而在很多rank相关领域如信息检索,更加关注的是topK的排序结果。
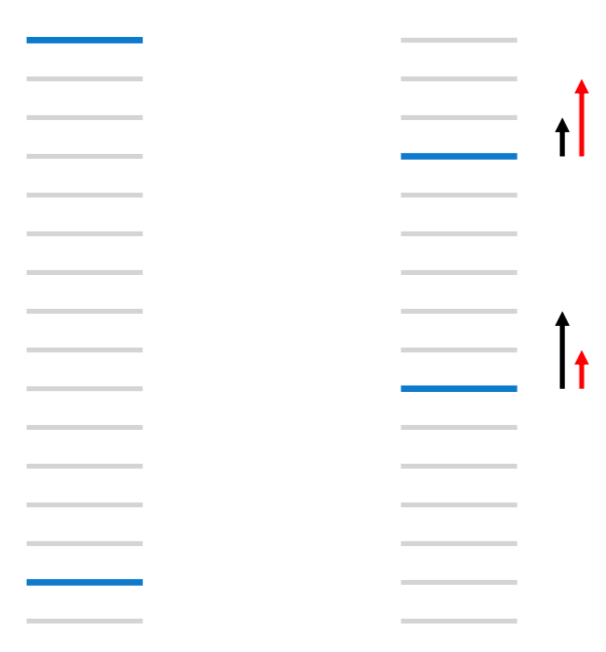
如下图所示,假定当前文档的相关性值只有0和1,灰色线表示和当前query不相关的文档,蓝色线表示和当前query相关文档,对于左图,pairwise误差为13,对于右图,将上面的相关文档下移3个位置,下面的相关文档上移5个位置,pairwise误差减少到11,而对于NDCG等更加关注top k结果的排序指标,误差可能是增加的。右图中的黑色箭头表示RankNet梯度方向,而我们更想要的是红色箭头对应的梯度方向。此时,就需要利用ListRank方法解决。
我们以LambdaRank方法为例,对Listwise进行说明。
LambdaRank
LambdaRank的建模和求解与RankNet类似。通过直接写出Cost对模型打分的梯度,而不是直接通过计算得到,是LambdaRank的主要思路。采用这样的思路,能绕过NDCG等排序指标对模型打分求导的困难。而$lambad$值正是代表对模型打分的梯度信息,每篇文档的$lambad$都从其它所有不同label的文档处获得其对应的更新方向和更新值。
对式10进行更新,乘于交换文档对$d_i$和$d_j$在rank列表中的位置后NDCG的变化幅度,能得到不错的结果[3]。
$\lambda_{ij}=\frac{\varphi C}{\varphi s_i}= \sigma (\frac{1}{2}(1-S_{ij})-\frac{1}{1+e^{-\sigma(s_i-s_j)}})|\triangle NDCG|$
由于每个query对应的文档对集合I中,前一个文档的相关性大于后一个,$S_{ij}=1$,因此,式12可以直接写成:
$\lambda_{ij}=\frac{\varphi C}{\varphi s_i}= \frac{-\sigma |\triangle NDCG|}{1+e^{-\sigma(s_i-s_j)}}) (12)$
经验表明,式12能直接优化NDCG指标。实际上,如果我们要优化其它指标,如MAP、MRR等,只需要更新NDCG的变化幅度为其它指标的变化幅度[3]。
LambdaMART
LambdaMART算法是LambdaRank和MART算法的组合。MART算法提供了算法的框架,需要用到的梯度相关信息则来自LambdaRank方法的梯度$y_i’=\lambda_i = \sum_{j:(i,j) \in I}\lambda_{ij}-\sum_{j:(j,i) \in I}\lambda_{ij}$
为方便描述,我们引入
$\sum_{(i,j) \doteq I} \lambda_{ij} = \sum_{j:(i,j) \in I}\lambda_{ij}-\sum_{j:(j,i) \in I}\lambda_{ij}$
$\lambda_i$相当于如下函数的导数:
$C=\sum_{(i,j) \doteq I}|\triangle NDCG_{ij}|log(1+e^{-\sigma(s_i-s_j)})$
$\frac{\varphi C}{\varphi s_i}= \sum_{(i,j) \doteq I}\frac{-\sigma |\triangle NDCG_{ij}|}{1+e^{-\sigma(s_i-s_j)}})= \sum_{(i,j) \doteq I} -\sigma |\triangle NDCG_{ij}|\rho_{ij}(13)$
其中$\rho_{ij}=\frac{1}{1+e^{-\sigma(s_i-s_j)}}$
$\frac{\varphi^2 C}{\varphi s_i^2}= \sum_{(i,j) \doteq I}\sigma^2 |\triangle NDCG_{ij}|\rho_{ij}(1-\rho_{ij})(14)$
对于第m棵树的第k个叶子结点,其对应的值如下:
$\gamma_{km}=\frac{\sum_{x_i \in R_{km}} \frac{\varphi C}{\varphi s_i}}{\sum_{x_i \in R_{km}} \frac{\varphi^2 C}{\varphi s_i^2}}=\frac{-\sum_{x_i \in R_{km}}\sum_{(i,j)\doteq I}|\triangle NDCG_{ij}|\rho_{ij}}{\sum_{x_i \in R_{km}}\sum_{(i,j)\doteq I}|\triangle NDCG_{ij}|\sigma\rho_{ij}(1-\rho_{ij})}$
LambdaMART算法的流程如下:

lambdaRank和lambadMART参数更新的不同:
前者对于每个query,计算梯度信息并更新一次参数,每次更新所有的模型参数;后者对每次分裂使用所有落在当前节点的样本及在同一group的样本,只更新当前节点的参数而非所有模型参数。
参考资料
[1] LI, Hang. “A Short Introduction to Learning to Rank”[J]. IEICE Transactions on Information and Systems, 2011.
[2] A. Shashua and A. Levin, “Ranking with large margin principle: Two approaches” in Advances in Neural Information Processing Systems 15, ed. S.T. S. Becker and K. Ober- mayer, MIT Press.
[3] Christopher J.C. Burges, “From RankNet to LambdaRank to LambdaMART: An Overview”, Microsoft Research Technical Report, 2010