矩阵分解模型的分布式求解

发表于   |   分类于   |   阅读次数

矩阵分解(mf)模型在推荐系统中有非常不错的表现，相对于传统的协同过滤方法，它不仅能通过降维增加模型的泛化能力，也方便加入其他因素（如数据偏差、时间、隐反馈等）对问题建模，从而产生更佳的推荐结果。本文主要介绍mf一些概念，基于sgd的mf分布式求解，基于als的mf分布式求解。
该文涉及的所有分布式求解都是基于openmit[1]的ps框架，因此分布式求解都是在ps基础上进行实现的。相对于spark mllib的mf实现，在同样的资源情况下，该框架下的实现能支持更大规模的矩阵分解。

矩阵分解相关概念

我们接触到很多的矩阵分解相关的一些概念，svd,pca,mf推荐模型,als等，如下是对这些概念的一些解释。

  • svd分解
    svd分解,是将一个矩阵A分解为三个矩阵，如下所示：
    $A_{m,n}=U_{m,m} I_{m,n} V_{n,n}^T (1)$
    其中矩阵$I$对角线元素为奇异值，对应$AA^T$的特征值的平方根。$U$的列为$MM^T$的特征向量(正交基向量)，称为$M$的左奇异向量。$V$的列为$M^TM$的特征向量(正交基向量)，称为$M$的右奇异向量。
    为了减少存储空间，可以用前$k$大的奇异值来近似描述矩阵$I$,$U$和$V^T$用对应前k大奇异值的左奇异向量和右奇异向量来近似，如下所示：
    $A_{m,n} \approx U_{m,k} I_{k,k} V_{k,n}^T (2)$

  • pca
    主成分分析，对原始数据进行降维使用。pca可以通过svd分解来实现，具体可以对公式(2)两边同时乘$V_{n,k}$,如下所示：
    $A_{m,n} V_{n,k} \approx U_{m,k} I_{k,k} V_{k,n}^T V_{n,k}$
    => $A_{m,n} V_{n,k} \approx U_{m,k} I_{k,k}$
    => $A_{m,n} V_{n,k} \approx A’_{m,k}(3)$
    经过公式3, 矩阵A由n列降为k列，如果要对行进行降维，其推导类似。

  • mf推荐模型
    在推荐领域，一般不直接使用svd进行矩阵分解，因为svd要求所有的矩阵元素不能缺失，而推荐所使用的的rating矩阵很难是完整的（互联网上的item经常海量的，一个user很难有机会接触所有的item, 导致user-item矩阵存在大量的元素缺失)。如果使用svd分解进行推荐，首先就需要对缺失的矩阵元素进行填充，不仅耗费大量的精力，而且填充的效果并不能保证准确。
    因此，对于个性化推荐，一般直接对已知的元素建立矩阵分解模型，如式4所示：
    $MIN_{PQ} \sum_{u,i\in\mathbb K} {(r_{ui} -
    p_u^Tq_i）}^2 + \lambda(p_u^Tp_u+q_i^Tq_i)（4）$
    对于(4)这样的建模，有些学者称为svd对已知元素建模(The goal of SVD, when restricted to the known ratings)[2].

  • als
    als（交替最小二乘）是一种矩阵分解优化算法。交替求解user向量和item向量，在求解user向量的时候固定item向量，在求解item向量的时候固定user向量，直到算法收敛或达到终止条件。
    als算法可用于求解矩阵分解模型模型如公式4, 也可用于更加灵活的矩阵分解模型，如隐反馈矩阵分解模型[3], 更加灵活地用于个性化推荐。

  • 非负矩阵分解[4]
    非负矩阵分解，是指将非负的大矩阵分解成两个非负的小矩阵。其目标函数和约束如下：
    $MIN_{PQ} \sum_{u,i\in\mathbb K} {(r_{ui} -
    p_u^Tq_i）}^2 （5）$
    $subject \; to \; r_{ui} \geq 0\;\; and \;\;p_{uk} \geq 0 \;\; and \;\; q_{ik} \geq 0 $
    相对于其他矩阵分解，非负矩阵分解的输入元素为非负，分解后矩阵的元素也非负。从计算上讲，虽然分解元素为负值是正确的，但是在很多情况下，在实际问题中是没有意义的。非负矩阵广泛应用于图像分析、文本聚类、语音处理、推荐系统等。

sgd求解in openmit

目标函数及优化推导

我们令$L=\sum_{u,i\in\mathbb K} {(r_{ui} -
p_u^Tq_i）}^2 + \lambda(p_u^Tp_u+q_i^Tq_i)$

对于user $u$和item $i$(rating大于0), 目标函数：$MIN_{PQ} (L)={(r_{ui} -
p_u^Tq_i）}^2 + \lambda(p_u^Tp_u+q_i^Tq_i)$

令$L$对$p_{u,k}$,$q_{i,k}$求导，如下所示：

$-\frac{1}{2}\frac{\varphi L}{\varphi p_{u,k}}=e_{u,i}q_{i,k}-\lambda p_{u,k}\;(6)$

$-\frac{1}{2}\frac{\varphi L}{\varphi q_{i,k}}=e_{u,i}p_{u,k}-\lambda q_{i,k}\;(7)$

其中$e_{u,i}=r_{ui} - p_u^Tq_i$。

利用梯度下降法迭代更新user向量p和item向量q, 如下所示：

$p_{u,k} = p_{u,k}+\alpha(e_{u,i}q_{i,k}-\lambda p_{u,k})\;(8)$

$q_{i,k} = q_{i,k}+\alpha(e_{u,i}p_{u,k}-\lambda q_{i,k})\;(9)$

分布式实现in openmit

在openmit中的矩阵存储模型如下图所示:

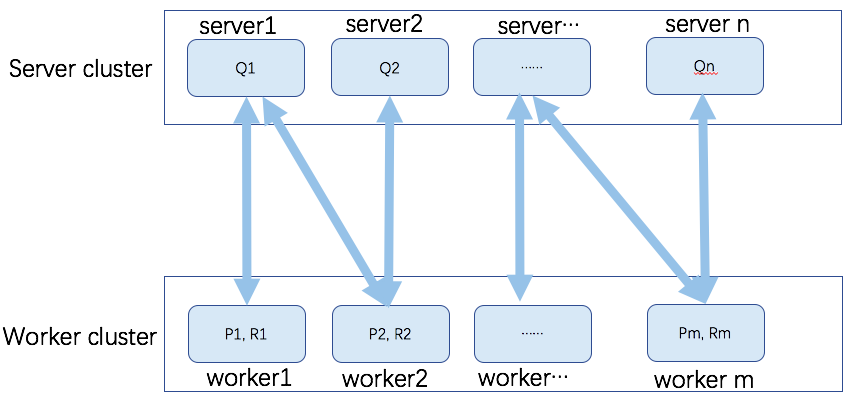
“矩阵存储模型”

图1：矩阵存储模型

我们假定user的数量远大于item数量，P矩阵代表user向量，Q矩阵代表item向量，R代表rating元素。此时我们将Q向量分布式存储在server集群，P向量分布式存储在worker集群，每个worker节点同时存储和该user相关联的rating元素R。

每个worker节点在计算user向量的时候，由于只需要用到本地user向量、与本地user相关的item向量和rating元素,而user向量和相关的rating元素存储在本地，因此只需要从server端拉取对应的item向量，就可以根据式6和式7完成user和item的梯度计算。利用公式8更新user向量，并将item梯度向量push给server集群，server端根据当前item向量权重，及worker端push的item梯度信息，根据式9更新item向量。具体流程参见如下描述:

worker端流程

1
2
3
4
5
6
7
8
9
10
11
12
//mf 分布式sgd求解woker端
load matrix rating data, each user data is loaded by only one worker;
for each epoch:
    for each batch:
        get batch data B;
        get user weights for users in B, (initialize user weights if not initialized)
        pull item weights from server
        for each user, item pair weith rating > 0:
            update user gradient according to eq 6;
            update item gradient according to eq 7;
        update user weights according to eq 8
        push item gradients to server

server端流程

1
2
3
4
5
6
7
8
9
10
//mf 分布式sgd求解server端
while(true):
    receive a requests from worker
    if request type is 'pull':
        if the item weights is not initialized:
            initialize the item weights;
        response the item weights to worker
    if request type is 'push':
        receive the item gradients
        update item weights accoreding to eq 9

当user的数量远小于item数量的时候，为需要减少通讯开销，需要更改输入文件，实现将item向量Q及rating元素R存储worker端，user向量P存储在server端。这样在进行数据传输的时候，worker端将会拉取user权重信息，push user梯度信息。通过传输user而非item信息，有效减少数据的通讯开销。

als求解in openmit

目标函数及优化推导

explicit als

explicit als只针对user-item矩阵中已知的rating元素进行建模，目标函数如式4所示，
我们令$L=\sum_{u,i\in\mathbb K} {(r_{ui} -
p_u^Tq_i）}^2 + \lambda(p_u^Tp_u+q_i^Tq_i)$

为求解user向量p, 固定所有item向量$q_i$, 令$L$对$p_u$求导等于0，

$-\frac{1}{2}\frac{\varphi L}{\varphi p_{u,k}} = 0$

=>$\sum_{i} (r_{ui} -
p_u^Tq_i）q_{i,k}-\lambda p_{u,k}=0\;$

=> $\sum_{i} (r_{ui} -
p_u^Tq_i）q_{i}-\lambda p_{u}=0\;$

=> $(\sum_iq_iq_i^T+\lambda I)p_u=\sum_iq_ir_{ui}\;(10)$

同理，为求解item向量q, 固定所有user向量$p_u$, 令$L$对$q_i$求导等于0，可得
$(\sum_up_up_u^T+\lambda I)q_i=\sum_up_ur_{ui}\;(11)$

对于式10和式11,利用cholesky分解的方法求解对应的$p$和$q$向量。

implicit als

对于所有的rating元素进行建模，通过$b_{ui}$建模user是否喜欢item, 通过$c_{ui}$建模user对item喜欢的程度，具体如下所示：

目标函数：$MIN_{P,Q}\sum_{u,i\in\mathbb K} c_{ui}{(b_{ui} -
p_u^Tq_i）}^2 + \lambda(p_u^Tp_u+q_i^Tq_i)\;\;(12)$

其中$b_{ui} = \begin{cases}
1, & r_{ui}>0\\
0, & r_{ui}=0
\end{cases}
$

$c_{ui} = 1 + \alpha r_{ui}$

令$L=\sum_{u,i\in\mathbb K} c_{ui}{(b_{ui} -
p_u^Tq_i）}^2 + \lambda(p_u^Tp_u+q_i^Tq_i)$

为求解user向量$p_u$, 固定所有item向量$q_i$, 令$L$对$p_u$求导等于0，
同时，对每个用户，引入$n\times n$矩阵$c^u$, $c^u_{ii}的值为c_{ui}$, 其余元素为0。

$-\frac{1}{2}\frac{\varphi L}{\varphi p_{u,k}} = 0$

=>$\sum_{i} c_{ui}(b_{ui} -
p_u^Tq_i）q_{i,k}-\lambda p_{u,k}=0\;$

=>$\sum_{i} c_{ui}(b_{ui} -
p_u^Tq_i）q_{i}-\lambda p_{u}=0\;$

=>$\sum_{i} c^u_{ii}b_{ui}q_i-c^u_{ii}p^T_uq_iq_i = \lambda p_u\;\;(13)$

其中:
$\sum_{i} c^u_{ii}b_{ui}q_i=Q^TC^ub_u\;(14)$

$\sum_{i} c^u_{ii}p^T_uq_iq_i = \sum_{i} q_i c^u_{ii}q^T_ip_u=Q^TC^uQp_u \;(15)$

其中$Q$的每一行表示每个item向量。

将式14和式15代入式13，得到：
$(Q^TC^uQ+\lambda I)p_u = Q^TC^ub_u\;(16)$

此时如果直接根据式16进行求解，假定item的个数为$n$, 每个item向量的维度为$f$, 对每个user向量的求解，仅$Q^TC^uQ$的计算就需要$O(f^2n)$.

在论文[3]中，作者使用了一种有效的加速方式，$Q^TC^uQ=Q^TQ+Q^T(C^u-I)Q$, 其中$Q^TQ$不依赖具体的用户，可以在计算所有user向量之前计算好，$C^u-I$只有$n_u$个对角线元素非零。由于$n_u ≪ n$，$Q^TC^uQ$的计算效率会明显提高。同理，由于$b_u$也只有$n_u$个非零值，$Q^TC^ub_u$的计算效率也会非常高。假定cholesky的求解需要$O(f^3)$,则每个user向量计算的复杂度为$O(f^2n_u+f^3)$

同理，为求解item向量$q_i$, 固定所有user向量$p_u$, 令$L$对$q_i$求导等于0, 可得：
$(P^TC^iP+\lambda I)q_i = P^TC^ib_i\;(17)$

分布式实现in openmit

als的分布式实现和sgd的分布式实现流程基本相似，不同之处在于每个worker阶段计算的不是user和item的梯度，而是通过cholesky分解直接计算出user和item的权重。

我们依然假设user的数量远远多于item的数量，worker端存储user权重和rating元素，server端存储item权重。worker端根据als计算出的user权重直接赋值给本地user向量，并将item权重push给server,由server直接赋值为新的item权重。

具体流程如下伪代码所示:

worker端流程

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
//mf 分布式als求解woker端
load matrix rating data, each user data loaded by only one worker;
for each epoch:
    for each batch:
        get batch data B;
        get user weights for users in B, (initialize user weights if not initialized)
        pull item weights from server
        pre compute Q'Q with item weight vector
        for each user:
            solve eq 16 by cholesky method to get user weight vector
            assign new user weight vector
        pre compute P'P with new user weight vector
        for each item:
            solve eq 17 by cholesky method to get item weight vector
        push item weight to server

server端流程

1
2
3
4
5
6
7
8
9
10
//mf 分布式als求解server端
while(true):
    receive a requests from worker
    if request type is 'pull':
        if the item weights is not initialized:
            initialize the item weights;
        response the item weights to worker
    if request type is 'push':
        receive the item weights
        assign new item weights vector

参考资料

[1]https://github.com/openmit/openmit
[2]Robert M. Bell, Yehuda Koren, “Scalable Collaborative Filtering with Jointly Derived Neighborhood Interpolation Weights”, IEEE International Conference on Data Mining, 2007,pp.43-52
[3]Yifan Hu, Yehuda Koren, Chris Volinsky, “Collaborative Filtering for Implicit Feedback Datasets”, Eighth IEEE International Conference on Data Mining, 2009,pp.263-272
[4]CJ Lin, “Projected Gradient Methods for Nonnegative Matrix Factorization”,《Neural Computation》,2007;19(10):2756